how to find sine of an angle
Tangent
Tangent, written every bit tan(θ), is 1 of the six cardinal trigonometric functions.
Tangent definitions
There are two main means in which trigonometric functions are typically discussed: in terms of right triangles and in terms of the unit of measurement circle. The correct-angled triangle definition of trigonometric functions is about often how they are introduced, followed by their definitions in terms of the unit circumvolve.
Right triangle definition
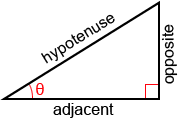
For a correct triangle with 1 acute angle, θ, the tangent value of this angle is defined to be the ratio of the opposite side length to the adjacent side length.
The sides of the right triangle are referenced as follows:
- Adjacent: the side adjacent to θ that is not the hypotenuse
- Contrary: the side opposite θ.
- Hypotenuse: the longest side of the triangle opposite the correct angle.
The other two most commonly used trigonometric functions are cosine and sine, and they are defined as follows:
Tangent is related to sine and cosine as:
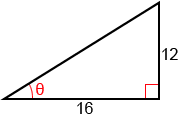
Example:
Find tan(θ) for the right triangle below.
Nosotros tin also use the tangent function when solving real world problems involving right triangles.
Example:
Jack is continuing 17 meters from the base of a tree. Given that the angle from Jack's anxiety to the superlative of the tree is 49°, what is the acme of the tree, h? If the tree falls towards Jack, volition it state on him?
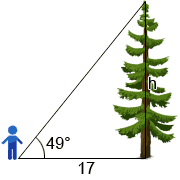
Since nosotros know the adjacent side and the angle, we tin use to solve for the height of the tree.
h = 17 × tan(49°) ≈ xix.56
So, the height of the tree is 19.56 chiliad. If Jack does not move, the tree will land on him if it falls in his direction, since 19.56 > 17.
Unit circumvolve definition
Trigonometric functions tin likewise exist defined with a unit circle. A unit circle is a circle of radius 1 centered at the origin. The correct triangle definition of trigonometric functions allows for angles between 0° and xc° (0 and in radians). Using the unit of measurement circle definitions allows united states of america to extend the domain of trigonometric functions to all real numbers. Refer to the effigy below.
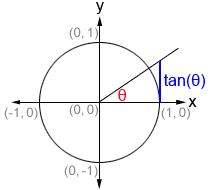
On the unit circle, θ is the angle formed between the initial side of an angle forth the 10-axis and the last side of the angle formed by rotating the ray either clockwise or counterclockwise. On the unit circle, tan(θ) is the length of the line segment formed by the intersection of the line x=one and the ray formed by the final side of the angle as shown in bluish in the effigy above.
Unlike the definitions of trigonometric functions based on right triangles, this definition works for any angle, not just astute angles of right triangles, as long equally it is within the domain of tan(θ), which is undefined at odd multiples of ninety° (). Thus, the domain of tan(θ) is θ∈R,
. The range of the tangent function is -∞<y<∞.
Values of the tangent function
At that place are many methods that tin can exist used to decide the value for tangent such as referencing a table of tangents, using a calculator, and approximating using the Taylor Series of tangent. In most applied cases, it is not necessary to compute a tangent value by hand, and a table, reckoner, or some other reference volition be provided.
Tangent calculator
The post-obit is a calculator to find out either the tangent value of an angle or the bending from the tangent value.
Commonly used angles
While we tin find tan(θ) for any angle, there are some angles that are more than frequently used in trigonometry. Beneath is a table of tangent values for commonly used angles in both radians and degrees.
| Angle in degrees | Angle in radians | Tangent value | Tangent value in decimals |
|---|---|---|---|
| 0° | 0 | 0 | 0 |
| fifteen° | | | 0.268 |
| 30° | | | 0.577 |
| 45° | | 1 | 1 |
| sixty° | | | 1.732 |
| 75° | | | 3.732 |
| 90° | | Undefined | Undefined |
| 180° | π | 0 | 0 |
| 270° | | Undefined | Undefined |
| 360° | 2π | 0 | 0 |
From these values, tangent tin be determined as . Cosine has a value of 0 at 90° and a value of 1 at 0°. On the other hand, sine has a value of 1 at 90° and 0 at 0°. Equally a result, tangent is undefined whenever cos(θ)=0, which occurs at odd multiples of xc° (
), and is 0 whenever sin(θ)=0, which occurs when θ is an integer multiple of 180° (π). The other normally used angles are xxx° (
), 45° (
), lx° (
) and their corresponding multiples. The cosine and sine values of these angles are worth memorizing in the context of trigonometry, since they are very commonly used, and can be used to decide values for tangent. Refer to the cosine and sine pages for their values.
Knowing the values of cosine, sine, and tangent for angles in the showtime quadrant allows us to determine their values for corresponding angles in the rest of the quadrants in the coordinate aeroplane through the use of reference angles.
Reference angles
A reference angle is an acute angle (<90°) that can exist used to represent an angle of whatsoever measure. Any angle in the coordinate plane has a reference angle that is between 0° and ninety°. Information technology is always the smallest angle (with reference to the x-axis) that tin can be made from the terminal side of an angle. The figure below shows an angle θ and its reference bending θ'.
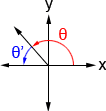
Because θ' is the reference bending of θ, both tan(θ) and tan(θ') have the aforementioned value. For example, 30° is the reference bending of 150°, and their tangents both have a magnitude of , admitting they accept different signs, since tangent is positive in quadrant I but negative in quadrant Ii. Considering all angles have a reference angle, we really merely need to know the values of tan(θ) (besides equally those of other trigonometric functions) in quadrant I. All other respective angles will have values of the same magnitude, and we just need to pay attention to their signs based on the quadrant that the terminal side of the angle lies in. Below is a table showing the signs of cosine, sine, and tangent in each quadrant.
| Tangent | Sine | Cosine | |
| Quadrant I | + | + | + |
| Quadrant II | - | + | - |
| Quadrant 3 | + | - | - |
| Quadrant Iv | - | - | + |
Once we determine the reference angle, we can determine the value of the trigonometric functions in whatsoever of the other quadrants by applying the appropriate sign to their value for the reference angle. The following steps can be used to find the reference angle of a given bending, θ:
- Subtract 360° or 2π from the bending equally many times as necessary (the angle needs to exist between 0° and 360°, or 0 and 2π). If the resulting angle is between 0° and 90°, this is the reference angle.
- Make up one's mind what quadrant the concluding side of the angle lies in (the initial side of the angle is along the positive x-axis)
- Depending what quadrant the concluding side of the angle lies in, use the equations in the table below to detect the reference bending. In quadrant I, θ'=θ.
| Quadrant II | Quadrant III | Quadrant IV |
|---|---|---|
 | 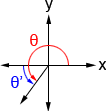 | 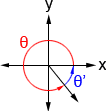 |
| θ'= 180° - θ | θ'= θ - 180° | θ'= 360° - θ |
Example:
Find tan(240°).
- θ is already between 0° and 360°
- 240° lies in quadrant III
- 240° - 180° = 60°, so the reference bending is lx°
tan(60°)=. 240° is in quadrant Three where tangent is positive, so: tan(240°)=tan(60°)=
Example:
Find tan(690°).
- 690° - 360° = 330°
- 330° lies in quadrant 4
- 360° - 330° = 30°
tan(30°) = . 330° is in quadrant 4 where tangent is negative, so:
tan(330°) = -tan(xxx°) =
Properties of the tangent part
Below are a number of properties of the tangent part that may exist helpful to know when working with trigonometric functions.
Tangent is a cofunction of cotangent
A cofunction is a function in which f(A) = g(B) given that A and B are complementary angles. In the context of tangent and cotangent,
tan(θ) = cot(90° - θ)
cot(θ) = tan(xc° - θ)
Example:
tan(30°) = cot(90° - thirty°)
tan(30°) = cot(lx°)
Referencing the unit circle shown higher up, the fact that , and
, nosotros can run into that:
tan(30°) = cot(60°) =
Tangent is an odd office
An odd part is a function in which -f(10)=f(-x). Information technology has symmetry most the origin. Thus,
-tan(θ) = tan(-θ)
Example:
-tan(30°) = tan(-30°)
-tan(30°) = tan(330°)
Referencing the unit circle or a table, nosotros can detect that tan(xxx°)=. tan(-30°) is equivalent to tan(330°), which we determine has a value of
. Thus, -tan(xxx°) = tan(330°) =
.
Tangent is a periodic function
A periodic part is a part, f, in which some positive value, p, exists such that
f(ten+p) = f(x)
for all x in the domain of f, p is the smallest positive number for which f is periodic, and is referred to as the period of f. The period of the tangent part is π, and it has vertical asymptotes at odd multiples of . We tin write this as:
tan(θ+π) = tan(θ)
To account for multiple full rotations, this can also exist written every bit
tan(θ+nπ) = tan(θ)
where n is an integer.
Dissimilar sine and cosine, which are continuous functions, each menstruum of tangent is separated past vertical asymptotes.
Case:
tan(405°) = tan(45° + ii×180°) = tan(45°) = 1
Graph of the tangent function
The graph of tangent is periodic, meaning that it repeats itself indefinitely. Unlike sine and cosine even so, tangent has asymptotes separating each of its periods. The domain of the tangent function is all real numbers except whenever cos(θ)=0, where the tangent part is undefined. This occurs whenever . This can exist written as θ∈R,
. Beneath is a graph of y=tan(ten) showing 3 periods of tangent.
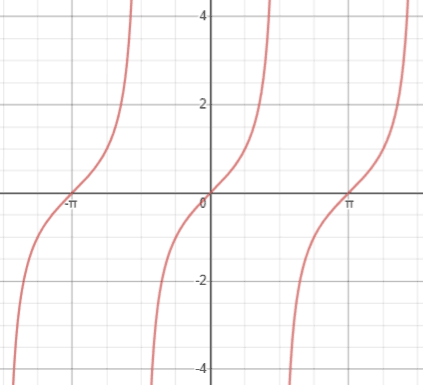
In this graph, we tin see that y=tan(x) exhibits symmetry near the origin. Reflecting the graph beyond the origin produces the same graph. This confirms that tangent is an odd function, since -tan(x)=tan(-10).
General tangent equation
The general form of the tangent function is
y = A·tan(B(10 - C)) + D
where A, B, C, and D are constants. To be able to graph a tangent equation in general grade, we need to outset understand how each of the constants affects the original graph of y=tan(10), equally shown above. To utilise anything written below, the equation must be in the form specified to a higher place; be conscientious with signs.
A—the amplitude of the function; typically, this is measured equally the height from the center of the graph to a maximum or minimum, as in sin(x) or cos(x). Since y=tan(x) has a range of (-∞,∞) and has no maxima or minima, rather than increasing the height of the maxima or minima, A stretches the graph of y=tan(10); a larger A makes the graph approach its asymptotes more apace, while a smaller A (<ane) makes the graph approach its asymptotes more slowly. This is sometimes referred to as how steep or shallow the graph is, respectively.
Compared to y=tan(x), shown in imperial below, the part y=5tan(x) (red) approaches its asymptotes more than steeply.
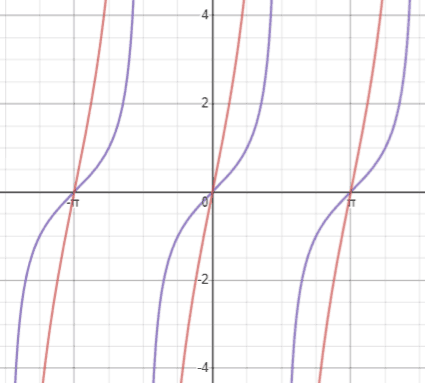
B—used to determine the period of the function; the period of a function is the distance from meridian to elevation (or whatever point on the graph to the next matching point) and can be found equally . In y=tan(x) the period is π. Nosotros tin confirm this by looking at the tangent graph. Referencing the effigy above, nosotros can run into that each period of tangent is bounded past vertical asymptotes, and each vertical asymptote is separated by an interval of π, so the menstruation of the tangent function is π.
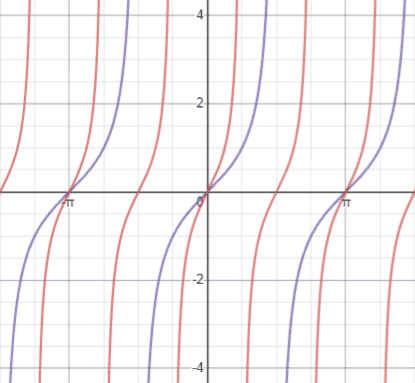
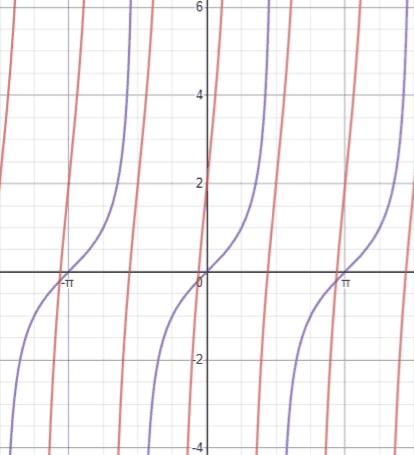
Compared to y=tan(x), shown in royal below, which has a period of π, y=tan(2x) (ruby) has a menses of . This means that the graph repeats itself every
rather than every π.
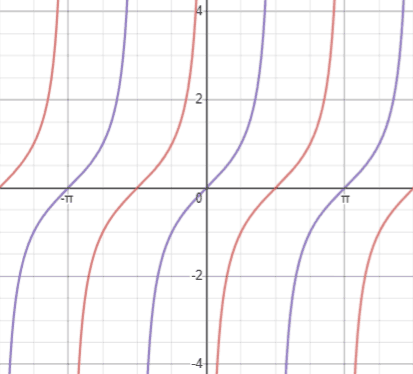
C—the phase shift of the role; phase shift determines how the function is shifted horizontally. If C is negative, the part shifts to the left. If C is positive the function shifts to the right. Be wary of the sign; if we have the equation then C is
non
, considering this equation in standard form is
. Thus, we would shift the graph
units to the left.
The effigy below shows y=tan(x) (purple) and (red). Using the zip of y=tan(ten) at (0, 0) as a reference, we can encounter that the aforementioned nil in
has been shifted to (
, 0).
D—the vertical shift of the function; if D is positive, the graph shifts up D units, and if it is negative, the graph shifts downwardly.
Compared to y=tan(x), shown in royal below, which is centered at the x-axis (y=0), y=tan(x)+2 (ruby-red) is centered at the line y=two (blue).
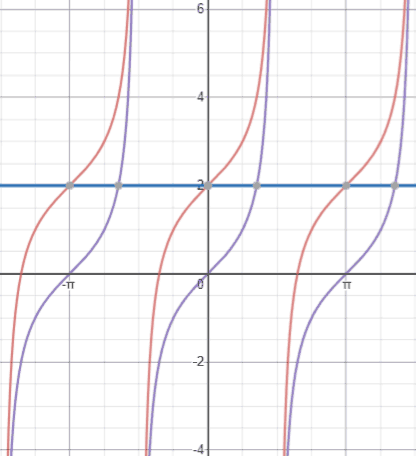
Putting together all the examples in a higher place, the figure below shows the graph of (red) compared to that of y=tan(ten) (purple).
See also sine, cosine, unit circumvolve, trigonometric functions, trigonometry.
Source: https://www.math.net/tangent
Posted by: johnsonsawn1984.blogspot.com

0 Response to "how to find sine of an angle"
Post a Comment